K moyennes.
Motivation
Identifier des groupes (clusters) dans un ensemble de données.
Analyse
L'algorithme des K-moyennes est un algorithme de ML non supervisé qui va associer à chaque point de `X` un groupe `{1..K}`.
Conception
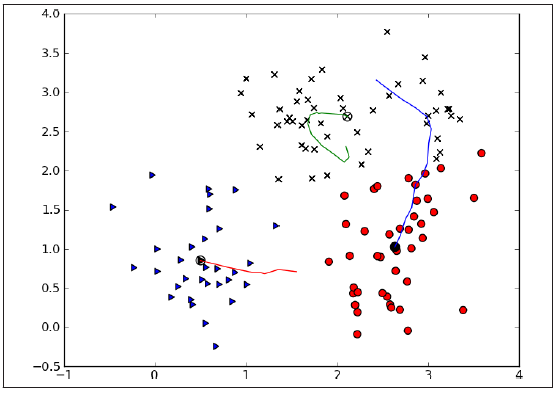
L'algorithme des K-moyennes consiste à associer des points à des groupes en fonction de leur distance à leurs barycentres (centroids) :
- tirer K points au hasard
- répéter jusqu'à convergence
- affecter des points aux groupes
- déplacer les barycentres des groupes
Affectation aux groupes
Pour déterminer le groupe (cluster) appartient (en attendant la convergence) chaque point `x^((i))` (avec `i` de 1 à `m`), on va chercher de quel barycentre `μ_k` il est le plus proche. On affectera alors à `c^((i))` l'indice du `k` groupe trouvé (par conséquent `μ_(c^((i)))` représente le barycentre auquel `x^((i))` est affecté).
Mathématiquement, cette opération revient à minimiser la fonction de coût suivante (dite "fonction de distorsion") sans changer les `μ_k` :
`J(c^((1)),…,c^((m)),μ_1,…,μ_K) = 1/m sum_(i=1)^m norm(x^((i))-μ_(c^((i))))^2`
Déplacement des barycentres
Déterminer pour chacun des K groupes `μ_k` qui est la moyenne des points (le nouveau barycentre) affectés au groupe `k` :
`μ_k:= 1/abs(Ck) sum_(i∈C_k)x^((i))` où `C_k` est l'ensemble de points affectés au barycentre `k`
Mathématiquement, cette opération revient à minimiser `J` par rapport aux `μ_k`.
Notes
- L'algorithme K-Means ne peut que converger.
- Le résultat trouvé ne sera pas forcément optimal, mais dépendra des points initialement choisis au hasard. C'est pour cela qu'il convient de réitérer l'algorithme avec des points initiaux différents et de choisir le cas qui aura donné une fonction J de coût minimale.
Exemples
Des exemples d'application de K-Means sont :
- Déterminer des segments de marché : par exemple à partir d'un ensemble de ventes de tee-shirts, déterminer quelles sont les populations pour des tailles S, M et L.
- Compresser une image : regrouper les couleurs d'une image en "groupes" et réduire ces couleurs à leur moyenne (permettant ainsi de passer de millions de couleurs 16 couleurs/groupes seulement par exemple).