Régression non linéaire

Motivation

• Déterminer si une variable quantitative (y) à une influence sur une autre (x)
• Prédire une valeur de y en fonction d'une valeur de x

Analyse

Soit :

• $X$ une matrice de $m\times n$ caractéristiques (features)
• $y$ un vecteur de données résultantes connues

Ce type de régression consiste à déterminer la fonction hypothèse $h_{\Theta }\left(x\right)={\Theta }_0+x{\Theta }_1$ dont les points sont les moins éloignés des valeurs réelles. Autrement dit déterminer les paramètres ${\Theta }_0$ et ${\Theta }_1$ qui permettent à la fonction linéaire h d'avoir des points ayant une distance/différence minimale avec les points "réels" (connus).

Conception

1. On détermine une fonction de coût permettant de calculer la différence entre h et y
2. On cherche à trouver ${\Theta }_0$ et ${\Theta }_1$ selon une méthode adaptée :
   • Descente de gradient si $n$ est grand
   • Equation normale si $n$ est relativement petit (< 1000) et si la matrice X est inversible (i.e. si m > n)

Notes

• Avant tout travail de modélisation, une approche descriptive ou exploratoire est nécessaire pour dépister au plus tôt des difficultés dans les données : dissymétrie des distributions, valeurs atypiques, liaison non linéaire entre les variables.
• Le modèle suppose implicitement une notion préalable de causalité dans le sens où Y dépend de X car le modèle n’est pas symétrique (i.e. X ne dépend pas forcément de Y).

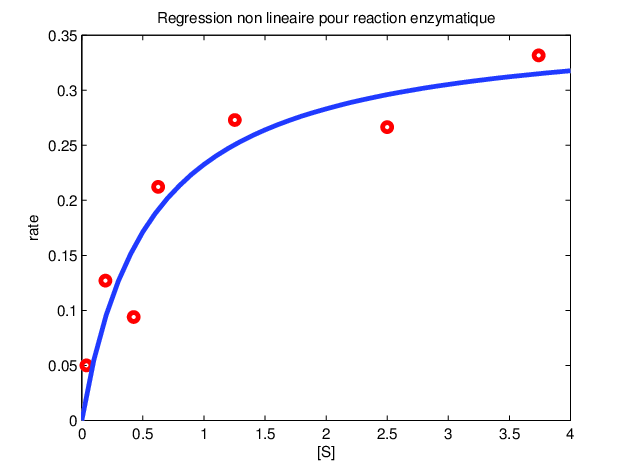
Exemples

• "Régression non linéaire dans Excel", 2017-10-20