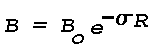
| Home > Rapport Condon > Sommaire > Le contexte scientifique > Mirage optique > Caractéristiques visuelles des phénomènes de réfraction de lumière dans l'atmosphère sans nuages |
|---|
An apparent optical image formed by light scattered out of a beam by a thin haze layer may be mistaken for a mirage. The theory of optical propagation in a scattering, attenuating atmosphere is well covered by Middleton (1952), an excellent reference containing much material on vision and the visibility of objects seen through the atmosphere.
The luminance or brightness, B, in e.g. lumens/m2 , of an extended object or optical source is invariant with distance except for losses due to scattering or absorption along the propagation path. Except under conditions of heavy fog, clouds, or smog, absorption is small compared to scattering, and Mai be neglected. If the scattering coefficient per unit length, O , is constant, attenuation of a light source of intrinsic brightness B is given by
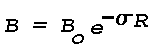
where R is the distance of range travelled by the light from the source to the point of observation. The portion of brightness lost by scattering out of the path is given by
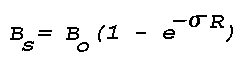
this loss represents light that is scattered in all directions by the molecules of air and aerosol particles present in the propagation path. Secondary scattering is neglected.
The quantity Sigma·R is often called the optical depth of an atmospheric layer, although it is a dimensionless quantity. Thus for thin layers where Sigma·R is small, the scattered light flux, F, in e.g. lumens, is
where F is the light flux incident on the layer.
The intensity, Is or light flux per unit solid angle, of the light scattered from a small volume of air, v, is the product of the incident light lfux, Fo, the volume scattering function, Beta'(Phi), and the average thickness of the volume. The scattering angle, Phi, is defined in Fig. 16. The intensity of light scattered at an angle Phi with respect to the incident beam is usually defined in terms of the incident illuminance, E, or flux per unit area in e.g., lumens/m2 on an element of volume dv. This results in
hence,
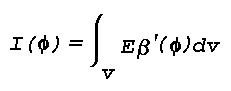
which, in the case of a small scattering volume where E and Beta'(Phi) Mai be considered nearly constant over the entire volume, reduces to
The units of Beta'(Phi) are typically lumens scattered per unit solid angle per unit volume per lumen incident light per unit area; I(Phi) then is expressed in candles, a unit of light intensity equal to one lumen per steradian. The volume scattering function is normalized by

hence for an isotropic scatterer, for which
The volume scattering function relative to an isotropic scatterer is conveniently defined as
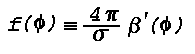
The relative volume scattering function for very clear air has maxima at
respectively, and a minimum of
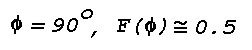
Industrial haze, or smog, has a strong maximum at
and a minimum at
with a weaker secondary maximum at

As an example of a scattering situation, consider a very clear atmosphere with a total vertical optical depth of 0.2; this is about twice the optical depth of a standard atmosphere of pure air (Middleton, (1952). The linear scattering coefficient, Phi, for this atmosphere will be about 2x10-5 m-1 near the ground. Assume that a haze layer one meter in thickness and with an optical depth of 0.02 exists at 100 m above the ground; the total optical depth of the composite atmosphere will be 0.22. The value of Sigma appropriate to the haze layer is 2x10-2 m-1, a factor of 103 greater than for the "clear" atmosphere above and below.
To an observer on the ground, the additional extinction of light caused by the presence of the haze layer, amounting to only 1.6% of the incident light from a source near the zenith, would not be perceptible except possibly very close to the horizon. However, light scattered out of an intense beam by the haze layer could be easily visible. Assume that a fairly powerful light source is aimed straight up from the ground; taking as typical values, e.g., for an automobile sealed beam unit, an intensity, Io, of 3x104 candles (30,000 candlepower) and a beam width of 6°, the light flux Fo incident on the layer at h = 100 m is 236 lumens, neglecting attenuation in the air below the layer. The beam solid angle, wo, is 7.85xl0-3 steradians. The incident illuminance, Eo, on the layer is
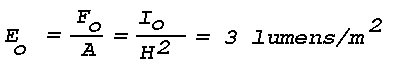
where the illuminated area, A = woh2, is 78.5m2. The scattering volume, v, is 78.5m3 since the layer is one meter thick, and the intensity of the scattered light is
If an observer is located 100 m from the light source, he will observe the scattered light at a distance of ~140 m and a scattering angle, Phi, of 135°. The apparent source of the scattered light will appear to be elliptical, roughly 4° wide and 3° high, and will present an area normal to the observer, An, of 62.6 m2. The value of f(Phi) for a strongly scattering medium at Phi = 135° is about 0.2; therefore the light Is scattered toward the observer is approximately 7.5x10-2 candles, and the apparent brightness, B, of the scattering volume will be
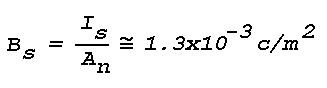
A fairly dark, moonless night sky has a background brightness, Bb of about 10-3 c/m2; the scattered image would therefore have a total brightness of ~2.2x10-3 c/m2 and a contrast against the night sky of
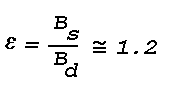
At this background brightness, data given by Middleton (1952) show that the contrast required for 50% probability of detection for an object of 3°-4° diameter is about 5.7x10-2; thus the image hypothesized in this example would have a brightness about 20 times greater than the minimum detectable, and would no doubt be easily visible as a pale, glowing, elliptical object.
In contrast, the air immediately above and below the haze layer with
Increasing the background brightness to 10-2 c/m2, corresponding to a bright, moonlit night,
would decrease the contrast of the scattered image to 1.2x10-1, which is about six times the minimum
detectable contrast at that background brightness and the image would therefore still constitute a fairly obvious
(object). Perception of light scattered from the rest of the beam under this increased background brightness, with
The level of background brightness for which the contrast of the image in this example would be reduced to the point where there is only a 50% probability of detection by an observer looking in the right direction is roughly 10-1 c/m2; this value corresponds to the brightness of a clear sky about 1/2 hour after sunset.
Thus, scattering of light from sources of small beam width by localized haze layers in the lower atmosphere Mai cause the appearance of diffuse, glowing patches of light, moving with movement of the light source, that could easily be interpreted as a UFO by an observer unfamiliar with such phenomena. Data given by Middleton (1952) show that with common light sources and under average nighttime sky conditions, the main beam of light could easily be imperceptible by scattered light, while at the same time the light scattered from a haze patch or layer would be easily visible to an observer; thus the source of the UFO-like image would not be apparent.
| Home > Rapport Condon > Sommaire > Le contexte scientifique > Mirage optique > Caractéristiques visuelles des phénomènes de réfraction de lumière dans l'atmosphère sans nuages |
|---|